1ª
LISTA DE EXERCÍCIOS COMPLEMENTARES DE MATEMÁTICA
Lembre-se
de que apesar de estar em casa, o compromisso, a
organização
e a dedicação com os estudos são muito importantes.
Tenha
um ótimo estudo!
1º)
Considerando o número 78.456.320, responda às perguntas:
a)
Quantas classes há nesse número?
b)
Quantas ordens há nesse número?
c)
Qual o algarismo das centenas de milhar?
d)
Qual é o nome da ordem ocupada pelo algarismo 7?
e)
e) Qual é o nome da ordem ocupada pelo algarismo 0?
f)
f) Qual é o nome da classe ocupada pelos algarismos 78?
g)
g) Quantas dezenas há nesse número?
2º)
Determine o valor posicional do algarismo 3 nos seguintes números:
a)
3.765
b)
32.000.000
c)
53.200.000.000
d)
890.123.000
3º)
Com os algarismos 2, 3 e 5 represente:
a)
o menor número de três algarismos;
b)
o menor número de três algarismos distintos;
c)
o menor de três algarismos diferentes que termina em 3.
4º)
Seguindo as pistas, descubra que número representa cada questão
abaixo:
a)
Pistas:
• O
algarismo das unidades é 1;
• O
algarismo das dezenas é o dobro do algarismo das unidades;
• O
algarismo das centenas é o dobro do algarismo das dezenas;
• O
algarismo dos milhares é o dobro do algarismo das centenas.
b)
Pistas:
• As
duas primeiras ordens trazem zeros;
• O
algarismo das centenas é 4;
• O
algarismo 7 tem valor posicional 7.000;
• O
algarismo de maior valor é 2;
• É
um número com 5 algarismos.
5º)
Determine:
a)
o antecessor do antecessor de 1.201;
b)
o sucessor do antecessor de 39;
c)
o antecessor do sucessor de 3.200;
d)
o sucessor do sucessor de 100.
6º)
(UECE) Dado um número de dois algarismos, forma-se um novo número
de três algarismos,
colocando
“1” à direita do número original. O novo número é (Assinale a
opção correta.)
a)
cem vezes o número original, mais um.
b)
dez vezes o número original, mais um.
c)
cem vezes o número original.
d)
o número original, mais um.
7º)
O IBGE apontou que a população de Goiás em 2008 era de 5.647.035
habitantes. Esse
número
tem (Assinale a opção correta.)
a)
8 algarismos e 3 classes.
b)
8 algarismos e 4 classes.
c)
7 algarismos e 3 classes.
d)
7 algarismos e 4 classes.
8º)
(OLIMPÍADA DE MATEMÁTICA-SP) No sistema decimal de numeração, um
número
tem
3 classes e 7 ordens. Então, esse número tem: (Assinale a opção
correta.)
a)
3 algarismos
b)
10 algarismos
c)
7 algarismos
d)
Nenhuma das anteriores
9º)
Usando os algarismos:
a)
Escreva o menor número, sem repetir nenhum algarismo.
b)
Escreve o maior número, sem repetir nenhum algarismo.
10º)
Observe as ordens nas etiquetas e escreva cada número usando
algarismos.
11º)
Dona Lourdes acabou de lavar umas camisetas. Para pendurar 4
camisetas no varal, usou 5
prendedores
de roupa. Quantos prendedores serão necessários para pendurar 18
camisetas?
12º)
Na semi-reta abaixo, os pontos marcados estão todos à mesma
distância uns dos outros.
Observe
os números representados e determine o valor de A, B, C, D e E.
0------1------B------3------.------D------A------7------.------E------.------10------.------C--.------14-------N>
|
13º)
Responda às perguntas:
a)
Qual é o menor número natural?
b)
Existe o maior número natural? Por quê?
c)
Todo número natural tem sucessor?
d)
Todo número natural tem antecessor?
14º)
Escreva o número formado por:
a)
Duas dezenas mais cinco unidades.
b)
Cinco centenas mais oito dezenas mais quatro unidades.
c)
Três dezenas de milhar mais seis unidades de milhar mais oito
unidades.
d)
Nove unidades de milhar mais nove dezenas.
15º)
(OBMEP-2007) Um número par tem 10 algarismos e a soma desses
algarismos é 89. Qual é o
algarismo
das unidades desse número? (Assinale a opção correta e justifique
sua resposta.)
a)
0
b)
2
c)
4
d)
6
e)
8
16º)
(OLIMPÍADA BRASILEIRA DE MATEMÁTICA) Qual dos números a seguir é
ímpar?
(Assinale
a opção correta, justificando sua resposta com os cálculos.)
a)
144 ÷ 36
b)
9 × 36
c)
37 – 23
d)
17 × 61
17º)
(Olimpíada de Matemática-CE) Maria está fazendo uma lista dos
números de três
algarismos,
escritos com os algarismos 7, 8 e 9, sem repeti-los. Quantos números
devem
aparecer
na lista de Maria? E quais são eles?
18º)
Complete a tabela a seguir:
ANTECESSOR
|
NÚMERO
|
SUCESSOR
|
385
|
||
699
|
||
3005
|
||
999
|
||
12982
|
19º)
Observe a seqüência de multiplicações:
a)
Escreva as duas próximas contas da seqüência. Dica: para descobrir
os produtos, você
não
precisa efetuar as multiplicações, basta perceber o padrão.
b)
A última conta dessa seqüência de multiplicações é 12.345.679 ×
81. Qual é seu resultado?
20º)
Observe a seqüência de figura:
Continuando
com esse padrão, quantos quadradinhos haverá na figura 6?
21º)
(Olimpíada de Matemática-CE) João escreveu vários números de
modo que, a partir terceiro,
cada
um é a soma dos dois últimos números escritos antes. Os cinco
primeiros números que ele
escreveu
foram: 1, 3, 4, 7 e 11. O próximo número será (Assinale a opção
correta
justifique
sua resposta.)
a)
17.
b)
19.
c)
20.
d)
18.
22º)
Qual é a próxima figura dessa seqüência figurada? Assinale X na
resposta certa.
23º)
(CEETEPS-SP) Nas figuras, cada X representa uma árvore que está
sendo cortada de forma
predatória,
a cada dia, conforme a seqüência apresentada.
No
sétimo dia, mantida a seqüência, o número de árvores cortadas
será:
24º)
Observe a seqüência de figuras:
Continuando
com esse padrão, quantas bolinhas haverá na figura 8? Justifique
sua
resposta.
25º)
Verifique qual das figuras abaixo corresponde a um número
triangular:
Agora,
escreva a seqüência dos 20 primeiros números triangulares.
26º)
Escreva por extenso os números abaixo:
a)
1.000.001
b)
2.703.000
a)
6.433.438.230
c)
120.001.001.001
d)
3.125.480
e)
15.845
f)
148.820.423.128
g)
156.568.789
h)
14.000.000
27º)
Escreva os números abaixo utilizando algarismos:
a)
Cento e oitenta e três milhões quinhentos e doze mil trezentos e
seis.
b)
Três milhões quarenta e três mil cento e sessenta e nove.
c)
Oito bilhões seiscentos e vinte e um milhões.
d)
Duzentos e doze trilhões oitenta e nove milhões cento e doze mil
trezentos e Noventa
e)
Oito quatrilhões e novecentos mil.
28º)
Represente os números abaixo na forma decomposta, conforme o
exemplo:
a)
25
b)
964
c)
4.552
d)
12.985
e)
188.302
f)
3.456.210
g)
12.860.154.890
Matemática 5ª série a) Relacione os elementos dos conjuntos A e B e escreva verdadeiro ou falso. ( ) 1 -Nenhum elemento do conjunto A é maior do que 1. ( ) 2 -Todos os elementos de B são maiores que zero. ( ) 3 -Nenhum elemento de B é menor do que 1. ( ) 4 -Todos os elementos de A são maiores que 10.17) Arme e efetue as operações abaixo:18) Calcule os quocientes abaixo com duas casas decimais:Cálculos: Cálculos:46 Nilo Alberto Scheidmandel Matemática 5ª sérieBibliografiaCASTRO, Alfredo e MULLER, Armando. Matemática Vol.1. Porto Alegre: Editora Movimento, 1981. DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005. SCHEIDMANDEL, Nilo Alberto. Organizador. Chapecó, 2008.
Máximo Divisor Comum
Dois números naturais sempre têm divisores comuns. Por exemplo: os divisores comuns de 12 e 18 são 1,2,3 e 6. Dentre eles, 6 é o maior. Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6.
O maior divisor comum de dois ou mais números é chamado de máximo divisor comum desses números. Usamos a abreviação m.d.c.
|
Alguns exemplos:
mdc (6,12) = 6
mdc (12,20) = 4
mdc (20,24) = 4
mdc (12,20,24) = 4
mdc (6,12,15) = 3
mdc (6,12) = 6
mdc (12,20) = 4
mdc (20,24) = 4
mdc (12,20,24) = 4
mdc (6,12,15) = 3
- CÁLCULO DO M.D.C.
Um modo de calcular o m.d.c. de dois ou mais números é utilizar a decomposição desses números em fatores primos.
1) decompomos os números em fatores primos;
2) o m.d.c. é o produto dos fatores primos comuns.
2) o m.d.c. é o produto dos fatores primos comuns.
Acompanhe o cálculo do m.d.c. entre 36 e 90:
36 = 2 x 2 x 3 x 3
90 = 2 x 3 x 3 x 5
36 = 2 x 2 x 3 x 3
90 = 2 x 3 x 3 x 5
O m.d.c. é o produto dos fatores primos comuns => m.d.c.(36,90) = 2 x 3 x 3
Portanto m.d.c.(36,90) = 18.
Portanto m.d.c.(36,90) = 18.
Escrevendo a fatoração do número na forma de potência temos:
36 = 22 x 32
90 = 2 x 32 x5
Portanto m.d.c.(36,90) = 2 x 32 = 18.
36 = 22 x 32
90 = 2 x 32 x5
Portanto m.d.c.(36,90) = 2 x 32 = 18.
O m.d.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns a eles, cada um elevado ao menor expoente.
|
- CÁLCULO DO M.D.C. PELO PROCESSO DAS DIVISÕES SUCESSIVAS
Nesse processo efetuamos várias divisões até chegar a uma divisão exata. O divisor desta divisão é o m.d.c. Acompanhe o cálculo do m.d.c.(48,30).
Regra prática:
1º) dividimos o número maior pelo número menor;
48 / 30 = 1 (com resto 18)
48 / 30 = 1 (com resto 18)
2º) dividimos o divisor 30, que é divisor da divisão anterior, por 18, que é o resto da divisão anterior, e assim sucessivamente;
30 / 18 = 1 (com resto 12)
30 / 18 = 1 (com resto 12)
18 / 12 = 1 (com resto 6)
12 / 6 = 2 (com resto zero - divisão exata)
3º) O divisor da divisão exata é 6. Então m.d.c.(48,30) = 6.
- NÚMEROS PRIMOS ENTRE SI
Dois ou mais números são primos entre si quando o máximo
divisor comum desses números é 1. |
Exemplos:
Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.
Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.
Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.
Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.
- PROPRIEDADE DO M.D.C.
Dentre os números 6, 18 e 30, o número 6 é divisor dos outros dois. Neste caso, 6 é o m.d.c.(6,18,30). Observe:
6 = 2 x 3
18 = 2 x 32
30 = 2 x 3 x 5
Portanto m.d.c.(6,18,30) = 6
18 = 2 x 32
30 = 2 x 3 x 5
Portanto m.d.c.(6,18,30) = 6
Dados dois ou mais números, se um deles é divisor de todos os outros, então
ele é o m.d.c. dos números dados. |
Veja também: Mínimo múltiplo comum (M.M.C.)
Mínimo Múltiplo Comum
- MÚLTIPLO DE UM NÚMERO NATURAL
Como 24 é divisível por 3 dizemos que 24 é múltiplo de 3.
24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.
24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.
Se um número é divisível por outro, diferente de zero, então
dizemos que ele é múltiplo desse outro. |
Os múltiplos de um número são calculados multiplicando-se esse número pelos números naturais.
Exemplo: os múltiplos de 7 são:
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...
Observações importantes:
1) Um número tem infinitos múltiplos
2) Zero é múltiplo de qualquer número natural
1) Um número tem infinitos múltiplos
2) Zero é múltiplo de qualquer número natural
- MÍNIMO MÚLTIPLO COMUM (M.M.C.)
Dois ou mais números sempre têm múltiplos comuns a eles.
Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.
O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.
|
- CÁLCULO DO M.M.C.
Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:
1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:
12 = 2 x 2 x 3
30 = 2 x 3 x 5 m.m.c (12,30) = 2 x 2 x 3 x 5
30 = 2 x 3 x 5 m.m.c (12,30) = 2 x 2 x 3 x 5
Escrevendo a fatoração dos números na forma de potência, temos:
12 = 22 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 22 x 3 x 5
12 = 22 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 22 x 3 x 5
O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores
comuns e não-comuns a eles, cada um elevado ao maior expoente. |
- PROCESSO DA DECOMPOSIÇÃO SIMULTÂNEA
| Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. Ao lado vemos o cálculo do m.m.c.(15,24,60) Portanto, m.m.c.(15,24,60) = 2 x 2 x 2 x 3 x 5 = 120 | 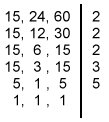 |
- PROPRIEDADE DO M.M.C.
Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c.(3,6,30). Observe:

m.m.c.(3,6,30) = 2 x 3 x 5 = 30
Dados dois ou mais números, se um deles é múltiplo de todos os outros, então
ele é o m.m.c. dos números dados. |
Considerando os números 4 e 15, ques são primos entre si. O m.m.c.(4,15) é igual a 60, que é o produto de 4 por 15. Observe:

m.m.c.(4,15) = 2 x 2 x 3 x 5 = 60
Dados dois números primos entre si, o m.m.c. deles é o produto desses números.
|
3 - POTENCIAÇÃO E RADICIAÇÃO
POTENCIAÇÃO
Consideremos uma multiplicação em que todos os fatores são iguais
Exemplo
5x5x5, indicada por 5³
ou seja , 5³= 5x5x5=125
onde :
5 é a base (fator que se repete)
3 é o expoente ( o número de vezes que repetimos a base)
125 é a potência ( resultado da operação)
Outros exemplos :
a) 7²= 7x7=49
b) 4³= 4x4x4=64
c) 5⁴= 5x5x5x5=625
d) 2⁵= 2x2x2x2x2=32
O expoente 2 é chamado de quadrado
O expoente 3 é chamado de cubo
O expoente 4 é chamado de quarta potência.
O expoente 5 é chamado de quinta potência.
Assim:
a) 7² Lê-se: sete elevado ao quadrado
b) 4³ Lê-se: quatro elevado ao cubo
c) 5⁴Lê-se: cinco elevado a quarta potência
d) 2⁵ Lê-se: dois elevado a quinta potência
Por convenção temos que:
1) todo o número elevado ao expoente 1 é igual à própria base,
exemplo
a) 8¹ = 8
b) 5¹ = 5
c) 15¹ = 15
2) todo o número elevado ao expoente zero é igual a 1
exemplo
a) 8º=1
b) 4º=1
c) 12º=1
EXERCÍCIOS
1) Em 7² = 49, responda:
a) Qual é a base?
b) Qual é o expoente?
c) Qual é a potência?
2) Escreva na forma de potência:
a) 4x4x4= (R: 4³)
b) 5x5 = (R: 5²)
c) 9x9x9x9x9= (R: 9⁵)
d) 7x7x7x7 = (R: 7⁴)
e) 2x2x2x2x2x2x2= (R: 2⁷ )
f) cxcxcxcxc= (R: c⁵ )
3) Calcule a potência:
a) 3² = (R: 9)
b) 8² = (R: 64)
c) 2³= (R: 8)
d) 3³ = (R: 27)
e) 6³ = (R: 216)
f) 2⁴ = (R: 16)
g) 3⁴ = (R: 81)
h) 3⁵ = (R: 243)
i) 1⁴ = (R: 1)
j) 0⁴ = (R: 0)
l) 1⁵ = (R: 1)
m) 10² = (R: 100)
n) 10³ = (R: 1000)
o) 15² = (R: 225)
p) 17² = (R: 289)
q) 30² = (R: 900)
4) Calcule as potências:
a)40² = (R: 1600)
b)32² = (R: 1024)
c)15³ = (R: 3375)
d) 30³= (R: 27000)
e) 11⁴ = (R: 14641)
f) 300² = (R: 90000)
g) 100³ = (R: 1000000)
h) 101² = (R: 10201)
5) Calcule as Potências:
a) 11² = (R: 121)
b) 20² = (R: 400)
c) 17² =(R: 289)
d) 0² = (R: 0)
e) 0¹ = ( R: 0)
f) 1⁶ = (R: 1)
g) 10³ = (R: 1.000)
h) 470¹ = (R: 470)
i) 11³ = R: 1331)
j) 67⁰ = (R: 1)
k) 1³⁰ = (R: 1)
l) 10⁵ = (R: 100000)
m) 1⁵ = (R: 1)
n) 15³ = (R: 3375)
o) 1² = (R: 1)
p) 1001⁰= (R: 1)
RADICIAÇÃO
Qual o número que elevado ao quadrado é igual a 9?
Solução
Sendo 3² = 9, podemos escrever que √9 = 3
Essa operação chama-se radiciação, que é a operação inversa da potenciação
Exemplos
Potenciação------------------------radiciação
a) 7² = 49 ---------------------------- √49= 7
b) 2³= 8 ------------------------------ ∛8 = 2
c) 3⁴= 81 ---------------------------- ∜81 = 3
O sinal √ chamamos de radical
O índice 2 significa : raiz quadrada
O índice 3 significa: raiz cúbica
O índice 4 significa: raiz quarta
assim:
√49= 7 lê-se: raiz quadrada de 49
∛8 = 2 lê-se : raiz cúbica de 8
∜81 = 3 lê-se: raiz quarta de 81
Nota:
Não é necessário o índice 2 no radical para a raiz quadrada
EXERCÍCIOS
1)Descubra o número que :
a) elevado ao quadrado dá 9
b) elevado ao quadrado dá 25
c) elevado ao quadrado dá 49
d) elevado ao cubo dá 8
2) Quanto vale x ?
a) x²= 9 (R:3)
b) x²= 25 (R:5)
c) x²= 49 (R:7)
d) x²= 81 (R:9)
3) Determine a Raiz quadrada:
a) √9 = (R: 3)
b) √16 = (R: 4)
c) √25 = (R: 5)
d) √81 = (R: 9)
e) √0 = (R: 0)
f) √1 = (R: 1)
g) √64 = (R: 8)
h) √100 = (R: 10)
4) Resolva as expressões abaixo:
a) √16 + √36 = 4 + 6 = (R: 10)
b) √25 + √9 = 5 + 3 = (R: 8)
c) √49 - √4 = 7 - 2 = (R: 5)
d) √36- √1 = 6 - 1 = (R: 5)
e) √9 + √100 = 3 + 10 = (R: 13)
f) √4 x √9 = 2 x 3 = (R: 6)
PROPRIEDADES DA POTENCIAÇÃO
Primeira propriedade
Multiplicação de potências de mesma base
Ao multiplicar potências de mesma base, repetimos a base e somamos os expoentes.
exemplos
3² x 3⁵ = 3²⁺⁵ = 3⁷
conclusão:
conservamos a base e somamos os expoentes.
EXERCÍCIOS
1) Reduza a uma só potência
a) 4³ x 4 ²= (R: 4⁵)
b) 7⁴ x 7⁵ = (R: 7⁹)
c) 2⁶ x 2²= (R: 2⁸)
d) 6³ x 6 = (R: 6⁴)
e) 3⁷ x 3² = (R: 3⁹)
f) 9³ x 9 = (R: 9⁴)
g) 5 x 5² = (R: 5³)
h) 7 x 7⁴ = (R: 7⁵)
i) 6 x 6 = (R: 6²)
j) 3 x 3 = (R: 3²)
l) 9² x 9⁴x 9 = (R: 9⁷)
m) 4 x 4² x 4 = (R: 4⁴)
n) 4 x 4 x 4= (R: 4³)
0) m⁰ x m x m³ = (R: m⁴)
p) 15 x 15³ x 15⁴x 15 = (R: 15⁹)
2) Reduza a uma só potência:
a) 7² x 7⁶ = (R: 7⁸)
b) 2² x 2⁴= (R: 2⁶)
c) 5 x 5³ = (R: 5⁴)
d) 8² x 8 = (R: 8³)
e) 3⁰ x 3⁰ = (R: 3⁰)
f) 4³ x 4 x 4² = (R: 4⁶)
g) a² x a² x a² = (R: a⁶)
h) m x m x m² = (R: m⁴)
i) x⁸ . x . x = (R: x¹⁰)
j) m . m . m = (R: m³)
Segunda Propriedade
Divisão de Potência de mesma base
Ao dividir potências de mesma base, repetimos a base e subtraímos os expoentes.
Exemplo
a) 8⁹: 8² = 8⁹⁻² = 8⁷
b) 5⁴ : 5 = 5⁴⁻¹ = 5³
conclusão : conservamos a base e subtraimos os expoentes
EXERCÍCIOS
1) Reduza a uma só potência
a) 5⁴ : 5² = (R: 5²)
b) 8⁷ : 8³ = (R: 8⁴)
c) 9⁵ : 9² = (R: 9³)
d) 4³ : 4² = (R: 4¹)
e) 9⁶ : 9³ = (R: 9³)
f) 9⁵ : 9 = (R: 9⁴)
g) 5⁴ : 5³ = (R: 5¹)
h) 6⁶ : 6 = (R: 6⁷)
i) a⁵ : a³ = (R: a²)
j) m² : m = (R: m¹)
k) x⁸ : x = (R: x⁷)
l) a⁷ : a⁶ = (R: a¹)
2) Reduza a uma só potência:
a) 2⁵ : 2³ =
b) 7⁸ : 7³=
c) 9⁴ : 9 =
d) 5⁹ : 5³ =
e) 8⁴ : 8⁰ =
f) 7⁰ : 7⁰ =
Teceira Propriedade
Potência de Potência
Ao elevar uma potência a um outro expoente, repetimos a base e multiplicamos os expoentes.
(7²)³ = 7²΄³ = 7⁶
conclusão: conservamos a base e multiplicamos os expoentes.
EXERCÍCIOS
1) Reduza a uma só potência:
a) (5⁴)²
b) (7²)⁴
c) (3²)⁵
d) (4³)²
e) (9⁴)⁴
f) (5²)⁷
g) (6³)⁵
h) (a²)³
i) (m³)⁴
j) (m³)⁴
k) (x⁵)²
l) (a³)⁰
m) (x⁵)⁰
2) Reduza a uma só potência:
a) (7²)³ =
b) (4⁴)⁵ =
c) (8³)⁵ =
d) (2⁷)³ =
e) (a²)³ =
f) (m³)⁴ =
g) (a⁴)⁴ =
h) (m²)⁷ =
EXPRESSÕES NUMÉRICAS COM POTENCIAÇÃO
Para resolver uma expressão numérica, efetuamos as operações obedecendo à seguinte ordem :
1°) Potenciação
2°) Multiplicações e divisões
3°) Adições e Subtrações
EXEMPLOS
1) exemplo
5 + 3² x 2 =
= 5 + 9 x 2 =
= 5 + 18 =
= 23
2) exemplo
7² - 4 x 2 + 3 =
= 49 – 8 + 3 =
= 41 + 3 =
= 44
Há expressões onde aparecem os sinais de associação e que devem ser eliminados nesta ordem:
1°) parênteses ( )
2°) colchetes [ ]
3°) chaves { }
exemplos
1°) exemplo
40 – [5² + ( 2³ - 7 )] =
= 40 – [5² + ( 8 - 7 )]
= 40 – [25 + 1 ]=
= 40 – 26 =
= 14
2°) exemplo
50 –{ 15 + [ 4² : ( 10 – 2 ) + 5 x 2 ] } =
= 50 –{ 15 + [ 16 : 8 + 10 ]}=
= 50 – { 15 + [ 2 + 10 ] } =
= 50 – { 15 +12 } =
= 50 – 27 =
= 23
Exercícios
1) Calcule o valor das expressões:
a) 7² - 4 = (R:45)
b) 2³ + 10 = (R:18)
c) 5² - 6 = (R:19)
d) 4² + 7⁰= (R:17)
e) 5⁰+ 5³= (R: 126)
f) 2³+ 2⁴ = (R: 24)
g) 10³ - 10² = (R: 900)
h) 80¹ + 1⁸⁰ = (R: 81)
i) 5² - 3² = (R: 16)
j) 1⁸⁰ + 0⁷⁰ = (R: 1)
2) Calcule
a) 3² + 5 = (R: 14)
b) 3 + 5² = (R: 28)
c) 3² + 5² = (R: 34)
d) 5² - 3² = (R: 16)
e) 18 - 7⁰ = (R: 17)
f) 5³ - 2² = (R: 121)
g) 10 + 10² = (R: 110)
h) 10³ - 10² = (R: 900)
i) 10³ - 1¹ = (R: 999)
3) Calcule o valor das expressões
a) 2³ x 5 + 3² = (R: 49)
b) 70⁰+ 0⁷⁰ - 1 = (R: 0 )
c) 3 x 7¹ - 4 x 5⁰ = (R: 17)
d) 3⁴- 2⁴: 8 – 3 x 4 = (R: 67)
e) 5² + 3 x 2 – 4 = (R: 27)
f) 5 x 2² + 3 – 8 = (R: 15)
g) 5² - 3 x 2² - 1 = (R: 12)
h) 16 : 2 – 1 + 7² = (R: 56)
4) calcule o valor das expressões:
a) 5² : ( 5 +1 -1)+ 4 x 2 = (R: 13)
b) (3 +1)² +2 x 5 - 10⁰ = (R: 25)
c) c) 3²: ( 4 – 1) + 3 x 2² = (R: 15)
d) 70 –[ 5 x (2² : 4) + 3²] = (R: 56)
e) ( 7 + 4) x ( 3² - 2³) = (R: 11)
f) 5² + 2³ - 2 x (3 + 9) = (R: 9)
g) 6² : 3² + 4 x 10 – 12 = (R: 32)
h) (7² - 1 ) : 3 + 2 x 5 = (R: 26)
5) calcule o valor das expressões:
a) 5 + 4²- 1 = (R: 20)
b) 3⁴ - 6 + 2³ = (R: 83)
c) 2⁵ - 3² + 1⁹ = (R: 24)
d) 10²- 3² + 5 = (R: 96)
e) 11² - 3² + 5 = (R: 117)
f) 5 x 3² x 4 = (R: 180)
g) 5 x 2³ + 4² = (R: 56)
h) 5³ x 2² - 12 = (R: 488)
6) Calcule o valor das expressões:
a) ( 4 + 3)² - 1 = (R: 48)
b) ( 5 + 1 )² + 10 = (R: 46)
c) ( 9 – 7 )³ x 8 = (R: 64)
d) ( 7² - 5²) + ( 5² - 3 ) = (R: 46)
e) 6² : 2 - 1⁴ x 5 = (R: 13)
f) 3² x 2³ + 2² x 5² = (R: 172)
7) Calcule o valor das expressões:
a) 4²- 10 + (2³ - 5) = (R: 9)
b) 30 – (2 + 1)²+ 2³ = (R: 29)
c) 30 + [6² : ( 5 – 3) + 1 ] = (R: 49)
d) 20 – [6 – 4 x( 10 - 3²) + 1] = (R: 17)
e) 50 + [ 3³ : ( 1 + 2) + 4 x 3] = (R: 71)
f) 100 –[ 5² : (10 – 5 ) + 2⁴ x 1 ] = (R: 79)
g) [ 4² + ( 5 – 3)³] : ( 9 – 7)³ = (R: 3 )
h) 7²+ 2 x[(3 + 1)² - 4 x 1³] = (R: 73)
i) 25 + { 3³ : 9 +[ 3² x 5 – 3 x (2³- 5¹)]} = (R: 64)
8) Calcule as expressões:
a) ( 8 : 2) . 4 + {[(3² - 2³) . 2⁴ - 5⁰] . 4¹}= (R:76)
b) ( 3² - 2³) . 3³ - 2³ + 2² . 4² = ( R:83)
c) ( 2⁵ - 3³) . (2² - 2 ) = (R: 10)
d) [2 . (10 - 4² : 2) + 6²] : ( 2³ - 2²) = ( R:10)
e) (18 – 4 . 2) . 3 + 2⁴ . 3 - 3² . ( 5 – 2) = (R: 51)
f) 4² . [2⁴ : ( 10 – 2 + 8 ) ] + 2⁰ = (R: 17)
g) [( 4² + 2 . 3²) + ( 16 : 8)² - 35]² + 1¹⁰ - 10⁰ = (R : 9)
h) 13 + ( 10 – 8 + (7 – 4)) = (R: 18)
i) (10 . 4 + 18 – ( 2 . 3 +6)) = (R:46)
j) 7 . ( 74 – ( 4 + 7 . 10)) = (R: 0)
k) ( 19 : ( 5 + 3 . 8 – 10)) = (R : 1)
l) (( 2³ + 2⁴) . 3 -4) + 3² = (R: 77)
m) 3 + 2 . ((3²- 2⁰) + ( 5¹ - 2²)) + 1 = (R: 22)
POTENCIAÇÃO
As principais operações são: adição, subtração, divisão e multiplicação. Utilizando o processo da multiplicação podemos encontrar outra operação: a potenciação, que para a realização de seus cálculos é necessário saber multiplicar.
Os números envolvidos em uma multiplicação são chamados de fatores e o resultado da multiplicação é o produto, quando os fatores são todos iguais existe uma forma diferente de fazer a representação dessa multiplicação que é a potenciação.
2 . 2 . 2 . 2 = 16 → multiplicação de fatores iguais.
Podemos representar a mesma multiplicação da seguinte forma:
2 . 2 . 2 . 2 = 24 = 16
↓
Fatores iguais.
Representamos uma potência da seguinte forma:
.jpg)
A base sempre será o valor do fator.
O expoente é a quantidade de vezes que o fator repete.
A potência é o resultado do produto.
introdução aos Números Naturais
O conjunto dos números naturais é representado pela letra maiúscula N e estes números são construídos com os algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, que também são conhecidos como algarismos indo-arábicos. No século VII, os árabes invadiram a Índia, difundindo o seu sistema numérico.
Embora o zero não seja um número natural no sentido que tenha sido proveniente de objetos de contagens naturais, iremos considerá-lo como um número natural uma vez que ele tem as mesmas propriedades algébricas que os números naturais. Na verdade, o zero foi criado pelos hindus na montagem do sistema posicional de numeração para suprir a deficiência de algo nulo. Para saber mais, clique nos links: Notas históricas sobre o zero ou Notação Posicional. Caso queira se aprofundar no assunto, veja o belíssimo livro: "História Universal dos Algarismos, Tomos I e II, Editora Nova Fronteira, 1998 e 1999", de Georges Ifrah.
Na sequência consideraremos que os naturais têm início com o número zero e escreveremos este conjunto como:
N = { 0, 1, 2, 3, 4, 5, 6, ...}
Representaremos o conjunto dos números naturais com a letra N. As reticências (três pontos) indicam que este conjunto não tem fim. N é um conjunto com infinitos números.
Excluindo o zero do conjunto dos números naturais, o conjunto será representado por:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
A construção dos Números Naturais
- Todo número natural dado tem um sucessor (número que vem depois do número dado), considerando também o zero.Exemplos: Seja m um número natural.
(a) O sucessor de m é m+1. (b) O sucessor de 0 é 1. (c) O sucessor de 1 é 2. (d) O sucessor de 19 é 20. - Se um número natural é sucessor de outro, então os dois números juntos são chamados números consecutivos.Exemplos:
(a) 1 e 2 são números consecutivos. (b) 5 e 6 são números consecutivos. (c) 50 e 51 são números consecutivos. - Vários números formam uma coleção de números naturais consecutivos se o segundo é sucessor do primeiro, o terceiro é sucessor do segundo, o quarto é sucessor do terceiro e assim sucessivamente.Exemplos:
(a) 1, 2, 3, 4, 5, 6 e 7 são consecutivos. (b) 5, 6 e 7 são consecutivos. (c) 50, 51, 52 e 53 são consecutivos. - Todo número natural dado n, exceto o zero, tem um antecessor (número que vem antes do número dado).Exemplos: Se m é um número natural finito diferente de zero.
(a) O antecessor do número m é m-1. (b) O antecessor de 2 é 1. (c) O antecessor de 56 é 55. (d) O antecessor de 10 é 9.
O conjunto abaixo é conhecido como o conjunto dos números naturais pares. Embora uma seqüência real seja um outro objeto matemático denominado função, algumas vezes utilizaremos a denominação sequência dos números naturais pares para representar o conjunto dos números naturais pares:
P = { 0, 2, 4, 6, 8, 10, 12, ...}
O conjunto abaixo é conhecido como o conjunto dos números naturais ímpares, às vezes também chamado, a sequência dos números ímpares.
I = { 1, 3, 5, 7, 9, 11, 13, ...}
Igualdade e Desigualdades
Diremos que um conjunto A é igual a um conjunto B se, e somente se, o conjunto A está contido no conjunto B e o conjunto B está contido no conjunto A. Quando a condição acima for satisfeita, escreveremos A=B (lê-se: A é igual a B) e quando não for satisfeita denotaremos tal fato por:

(lê-se: A é diferente de B). Na definição de igualdade de conjuntos, vemos que não é importante a ordem dos elementos no conjunto.
Exemplo com igualdade: No desenho, em anexo, observamos que os elementos do conjunto A são os mesmos elementos do conjunto B. Neste caso, A=B.

Consideraremos agora uma situação em que os elementos dos conjuntos A e B serão distintos.
Sejam A={a,b,c,d} e B={1,2,3,d}. Nem todos os elementos do conjunto A estão no conjunto B e nem todos os elementos do conjunto B estão no conjunto A. Também não podemos afirmar que um conjunto é maior do que o outro conjunto. Neste caso, afirmamos que o conjunto A é diferente do conjunto B.
Exercício: Há um espaço em branco entre dois números em cada linha. Qual é o sinal apropriado que deve ser posto neste espaço: <, > ou =?
| 159 | 170 | |
|---|---|---|
| 852 | 321 | |
| 587 | 587 |
Exercício: Representar analiticamente cada conjunto, isto é, através de alguma propriedade e depois por extensão, apresentando os elementos:
- Conjunto N dos números Naturais
- Conjunto P dos números Naturais Pares
- Conjunto I dos números Naturais Ímpares
- Conjunto E dos números Naturais menores que 16
- Conjunto L dos números Naturais maiores que 11
- Conjunto R dos números Naturais maiores ou iguais a 28
- Conjunto C dos números Naturais que estão entre 6 e 10
Operações com Números Naturais
Na sequência, estudaremos as duas principais operações possíveis no conjunto dos números naturais. Praticamente, toda a Matemática é construída a partir dessas duas operações: adição e multiplicação.
A adição de números naturais
A primeira operação fundamental da Aritmética, tem por finalidade reunir em um só número, todas as unidades de dois ou mais números. Antes de surgir os algarismos indo-arábicos, as adições podiam ser realizadas por meio de tábuas de calcular, com o auxílio de pedras ou por meio de ábacos.

Propriedades da Adição
- Fechamento: A adição no conjunto dos números naturais é fechada, pois a soma de dois números naturais é ainda um número natural. O fato que a operação de adição é fechada em N é conhecido na literatura do assunto como: A adição é uma lei de composição interna no conjunto N.

- Associativa: A adição no conjunto dos números naturais é associativa, pois na adição de três ou mais parcelas de números naturais quaisquer é possível associar as parcelas de quaisquer modos, ou seja, com três números naturais, somando o primeiro com o segundo e ao resultado obtido somarmos um terceiro, obteremos um resultado que é igual à soma do primeiro com a soma do segundo e o terceiro.

- Elemento neutro: No conjunto dos números naturais, existe o elemento neutro que é o zero, pois tomando um número natural qualquer e somando com o elemento neutro (zero), o resultado será o próprio número natural.

- Comutativa: No conjunto dos números naturais, a adição é comutativa, pois a ordem das parcelas não altera a soma, ou seja, somando a primeira parcela com a segunda parcela, teremos o mesmo resultado que se somando a segunda parcela com a primeira parcela.

Curiosidade: Tabela de adição
Para somar dois números, com a tabela, um em uma linha e outro em uma coluna, basta fixar um número na 1a. coluna e um segundo número na 1a. linha. Na interseção da linha e coluna fixadas, obtemos a soma dos números.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
Por exemplo, se tomarmos o número 7 na linha horizontal e o número 6 na linha vertical, obteremos a soma 13 que está no cruzamento da linha do 7 com a coluna do 6.
Multiplicação de Números Naturais
É a operação que tem por finalidade adicionar o primeiro número denominado multiplicando ou parcela, tantas vezes quantas são as unidades do segundo número denominado multiplicador.
Exemplo: 4 vezes 9 é somar o número 9 quatro vezes:
4 x 9 = 9 + 9 + 9 + 9 = 36
O resultado da multiplicação é denominado produto e os números dados que geraram o produto, são chamados fatores. Usamos o sinal × ou · ou x, para representar a multiplicação.
Propriedades da multiplicação
- Fechamento: A multiplicação é fechada no conjunto N dos números naturais, pois realizando o produto de dois ou mais númros naturais, o resultado estará em N. O fato que a operação de multiplicação é fechada em N é conhecido na literatura do assunto como: A multiplicação é uma lei de composição interna no conjunto N.

- Associativa: Na multiplicação, podemos associar 3 ou mais fatores de modos diferentes, pois se multiplicarmos o primeiro fator com o segundo e depois multiplicarmos por um terceiro número natural, teremos o mesmo resultado que multiplicar o terceiro pelo produto do primeiro pelo segundo.(m.n).p = m.(n.p)
(3.4).5 = 3.(4.5) = 60 - Elemento Neutro: No conjunto dos números naturais existe um elemento neutro para a multiplicação que é o 1. Qualquer que seja o número natural n, tem-se que:1.n = n.1 = n
1.7 = 7.1 = 7 - Comutativa: Quando multiplicamos dois números naturais quaisquer, a ordem dos fatores não altera o produto, ou seja, multiplicando o primeiro elemento pelo segundo elemento teremos o mesmo resultado que multiplicando o segundo elemento pelo primeiro elemento.m.n = n.m
3.4 = 4.3 = 12
Propriedade Distributiva
Multiplicando um número natural pela soma de dois números naturais, é o mesmo que multiplicar o fator, por cada uma das parcelas e a seguir adicionar os resultados obtidos.

m.(p+q) = m.p + m.q
6x(5+3) = 6x5 + 6x3 = 30 + 18 = 48
6x(5+3) = 6x5 + 6x3 = 30 + 18 = 48
Divisão de Números Naturais
Dados dois números naturais, às vezes necessitamos saber quantas vezes o segundo está contido no primeiro. O primeiro número que é o maior é denominado dividendo e o outro número que é menor é o divisor. O resultado da divisão é chamado quociente. Se multiplicarmos o divisor pelo quociente obteremos o dividendo.
No conjunto dos números naturais, a divisão não é fechada, pois nem sempre é possível dividir um número natural por outro número natural e na ocorrência disto a divisão não é exata.
Relações essenciais numa divisão de números naturais
- Em uma divisão exata de números naturais, o divisor deve ser menor do que o dividendo.35 : 7 = 5
- Em uma divisão exata de números naturais, o dividendo é o produto do divisor pelo quociente.35 = 5 x 7
- A divisão de um número natural n por zero não é possível pois, se admitíssemos que o quociente fosse q, então poderiamos escrever:n ÷ 0 = qe isto significaria que:n = 0 x q = 0o que não é correto! Assim, a divisão de n por 0 não tem sentido ou ainda é dita impossível.
Exercício: Substituindo X por 6 e Y por 9, qual é o valor da soma do dobro de X pelo triplo de Y.
Potenciação de Números Naturais
Para dois números naturais m e n, a expressão mn é um produto de n fatores iguais ao número m, ou seja:
mn = m . m . m ... m . m
m aparece n vezes
m aparece n vezes
O número que se repete como fator é denominado base que neste caso é m. O número de vezes que a base se repete é denominado expoente que neste caso é n. O resultado é donominado potência.
Esta operação não passa de uma multiplicação com fatores iguais, como por exemplo:
23 = 2 × 2 × 2 = 8
43 = 4 × 4 × 4 = 64
43 = 4 × 4 × 4 = 64
Propriedades da Potenciação
- Uma potência cuja base é igual a 1 e o expoente natural é n, denotada por 1n, será sempre igual a 1.Exemplos:
- 1n = 1×1×...×1 (n vezes) = 1
- 13 = 1×1×1 = 1
- 17 = 1×1×1×1×1×1×1 = 1
- Se n é um número natural não nulo, então temos que no=1. Por exemplo:
(a) nº = 1 (b) 5º = 1 (c) 49º = 1 - A potência zero elevado a zero, denotada por 0o, é carente de sentido no contexto do Ensino Fundamental. O visitante que necessitar aprofundamento neste assunto, deve visitar nosso link Zero elevado a zero?
- Qualquer que seja a potência em que a base é o número natural n e o expoente é igual a 1, denotada por n1, é igual ao próprio n. Por exemplo:
(a) n¹ = n (b) 5¹ = 5 (c) 64¹ = 64 - Toda potência 10n é o número formado pelo algarismo 1 seguido de n zeros.Exemplos:
- 103 = 1000
- 108 = 100.000.000
- 10o = 1
Potenciação com o browser
Para obter uma potência Mn com o Browser Netscape, como por exemplo 125, digite (ou copie com Control+C) a linha de comando:
javascript:Math.pow(12,5)
exatamente da forma como está escrito, na caixa que aparece em seu browser com o nome do arquivo que está sendo acessado neste momento (location=endereço). Após isto, pressione a tecla ENTER. Você verá uma nova janela com a resposta
248832
Para sair da janela com a resposta, pressione o botão Voltar (Back) de seu browser.
Números grandes
No livro "Matemática e Imaginação", o matemático americano Edward Kasner apresentou um número denominado googol que pode ser representado por 1 seguido de 100 zeros.
1 Googol = 10100
Ele pensou que este era um número superior a qualquer coisa que passasse pela mente humana sendo maior do que qualquer coisa que pode ser posta na forma de palavras. Um googol é um pouco maior do que o número total de partículas elementares conhecidas no universo, algo da ordem de 1080. Se o espaço com estas partículas fosse comprimido de uma forma sólida com neutrons, este ficaria com algo em torno de 10128partículas.
Outro matemático criou então o googolplex e o definiu como 10 elevado ao googol.
1 Googolplex = 10Googol
Exercícios
- Na figura abaixo, insira os números 1, 2, 3, 4, 5 e 6 nos círculos, de tal modo que a soma de cada lado seja sempre igual a 10.

- Um gavião viu um grupo de pombos, chegou perto deles e disse:
Olá minhas 100 pombinhas. Uma delas respondeu: Não somos 100 não meu caro gavião, seremos 100, nós, mais dois tantos de nós e mais você meu caro gavião. Quantos pombos há neste grupo? - Três homens querem atravessar um rio. O barco que eles possuem suporta no máximo 150 kg. Um deles pesa 50 kg, o segundo pesa 75 kg e o terceiro pesa 120 kg. Qual será o processo para eles atravessarem o rio sem afundar?
- Forme um quadrado mágico com os números 1, 2, 3, 4, 5, 6, 7, 8 e 9 tal que, a soma dos números de qualquer linha, qualquer coluna ou qualquer diagonal deverá ser sempre igual a 15.
http://pessoal.sercomtel.com.br/matematica/fundam/naturais/naturais1.htm














Nenhum comentário:
Postar um comentário